超音波共鳴法による機能性薄膜の異方性弾性定数の測定

近年，電子デバイスの小型軽量化と高性能化を実現するために多くの電子デバイスにおいて薄膜が使用されています．　デバイスの設計では薄膜の機械的性質を把握する必要がありますが，中でも弾性定数は設計のキーパラメータのひとつであります．　たとえば表面弾性波（surface acoustic wave: SAW）フィルタにおいては，中心周波数がSAWの速度に依存するため，圧電薄膜の弾性定数が支配的パラメータとなります．　また，SAW速度は櫛型電極の影響も受けるため，電極として使われる薄膜の弾性定数を把握する必要があります．　さらに，薄膜は基板上に成膜された状態で使用されますが，温度変化の生じる環境下では薄膜と基板の線膨張係数の違いによって熱応力が生じます．　この熱応力の解析においても薄膜の弾性定数は不可欠です． 　薄膜の弾性定数を測定することは，上記のようにデバイスの設計に直接的な指針を与えるだけでなく，薄膜の内部組織を非破壊的に評価することにもつながります．　薄膜はしばしば内部に不完全結合部や微細な欠陥を含んでおり，多結晶薄膜であれば結晶粒界に不完全結合部を生じることがあります．　このような微小欠陥はデバイスの性能や信頼性を低下させるため，その体積分率や形状・方位を把握することが重要な課題でありますが，これらは電子顕微鏡観察など他の手法では評価することが困難です．　しかしながら，巨視的弾性定数はこれらの欠陥に敏感であるため，弾性定数の測定から欠陥を評価することが可能になります． 　上述のように，薄膜の弾性定数を測定することは学術的興味だけでなく，今後のデバイス開発に大きく貢献することが期待されており，これまでにもさまざまな手法を用いて薄膜の弾性定数測定が行われています．　しかしながら，薄膜の弾性的性質に関する系統的かつ詳細な研究は十分には行われていません．　この理由としては以下の2つが挙げられます．

原理的に異方性弾性定数を決定することができない． 異方性を検出できるほど弾性定数の測定精度が高くない． 　まず，「原理的に異方性弾性定数を決定することができない」についてですが，その前に薄膜の弾性異方性について考えてみましょう．　実際の薄膜は残留応力や集合組織，結晶粒間の不完全結合，柱状組織の影響を受けて，面内方向と膜厚方向に対して異方性を示します（面内は等方性です）．　このような弾性対称性は面内等方性（六方晶系の単結晶金属と同様の弾性対称性）と呼ばれ，独立な弾性定数は5つ存在します（等方体の独立な弾性定数は2つ）．　薄膜の膜厚方向をx3軸とし，面内方向にx1，x2軸を定義した場合，弾性定数マトリックスはFig.1に示す形になります．

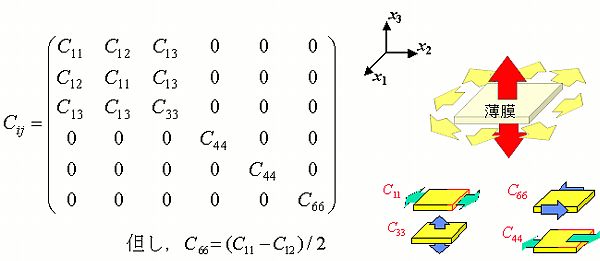
上記のように薄膜には5つの独立な弾性定数が存在しますが，従来の測定法ではほとんどの場合において薄膜を等方体と仮定します．　例えば，マイクロ引っ張り試験で5つの弾性定数を決定するためには薄膜を面内方向に引っ張るだけでなく，膜厚方向や斜め上方向など，最低でも5つの異なる方向に対して引っ張り試験を行う必要があります（5つの未知数（弾性定数）を求めるためには，最低でも5つの独立な関係式が必要なため）．　しかしながら，そのような測定は実際には不可能です．　また，等方体の解析モデルに比べて，異方性を考慮した解析モデルが複雑であることも異方性弾性定数の測定を困難なものにしています． 　「異方性を検出できるほど弾性定数の測定精度が高くない」という点については，従来法では試料の保持や寸法誤差が測定結果に大きく影響することが挙げられる．ために，弾性異方性について議論することは容易ではありません．　特に静的な測定法（マイクロ曲げ，引っ張り試験）では試料寸法が3乗のオーダーで弾性定数に影響するため，寸法の測定誤差によって得られる弾性定数が大きく変化します．

本研究では薄膜の異方性弾性定数を測定する手法として共鳴超音波スペクトロスコピー（resonant-ultrasound spectroscopy: RUS）を提案しています．　RUSとは固体の自由振動の共鳴周波数から弾性定数を決定する手法であり，原理的には全ての独立な弾性定数を決定することができます．　Fig.2に測定の概念図を示します．基板上に薄膜を成膜した層状材料を自由振動させると，特定の周波数で共鳴振動が生じます．　共鳴振動が生じる周波数は無数に存在しており，共鳴周波数と呼ばれています．　この共鳴周波数は基板と薄膜の寸法，密度および弾性定数によって決まります（Fig.2，上）．従って，共鳴周波数を測定することで薄膜の弾性定数を測定することができます（Fig.2，下）．

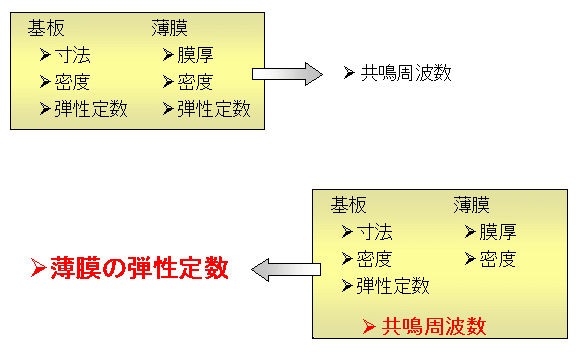
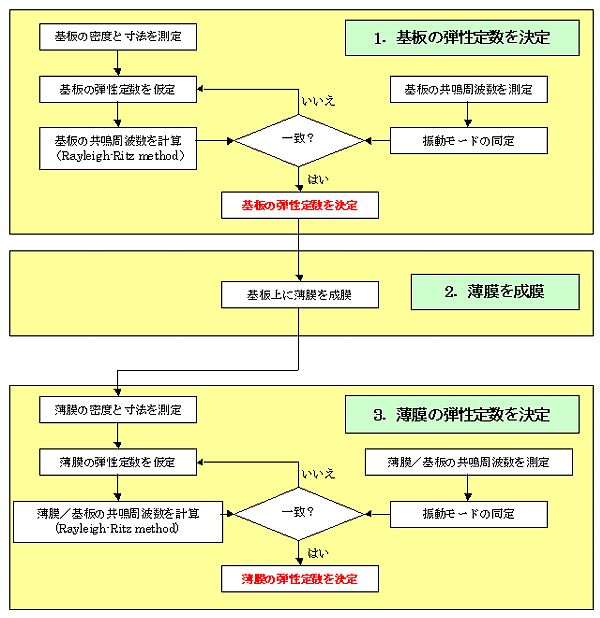
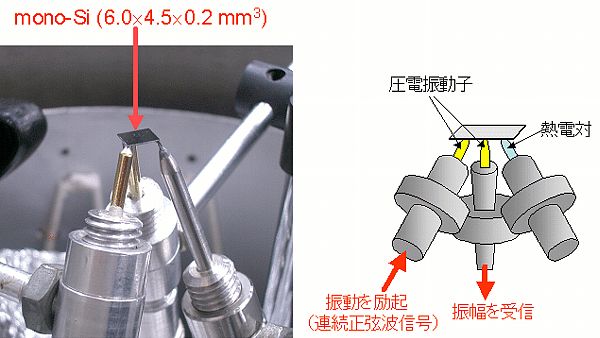
RUSの特徴は何と言っても「固体の自由振動」を利用する点です．　自由振動では複雑な境界条件を考える必要がなく，Rayleigh-Ritz法によって簡単かつ精度良く共鳴周波数や振動振幅を計算することができます．　（他の手法では，試料を保持することによって境界条件が複雑になります．　また，ナノインデンテーションなどではインデンテーターの形状や弾性定数など，解析に必要なパラメータが非常に多く，測定誤差を含みやすくなっています．） 　RUSによる薄膜の弾性定数の測定手順は大きく3つに分かれています． 基板単体の共鳴周波数を測定し，基板の弾性定数を決定する． 基板上に薄膜を成膜する． 成膜後の基板の共鳴周波数を再度測定し，薄膜の弾性定数を決定する． 　RUSでは，最初に基板の弾性定数を決定します．現在（2006年4月10日）主に使用している基板は単結晶シリコンで，基板の寸法はおよそ6.0×4.5×0.2 mm3です．　まず，基板の寸法をマイクロメーターで測定します．　マイクロメーターによる測定誤差は2～3mm程度であり，面内方向と膜厚方向の寸法誤差はそれぞれおよそ 0.05%，1.5% となります．　また，質量を電子天秤で測定して密度を算出します．　その後，基板の弾性定数を真値に近いと思われる値で仮定して共鳴周波数を計算します．　この共鳴周波数の計算値を測定値と比較し，両者が十分一致するまで基板の弾性定数を変えながら共鳴周波数を計算します（最小二乗法を用いて弾性定数を収束させます）．　そして，両者が十分一致したときの弾性定数を基板の弾性定数として決定します（この計算過程を逆計算と呼ぶことにします）．　この逆計算には約20個の共鳴周波数を使用し，共鳴周波数の計算値と測定値のrms errorは0.1%以下です．　弾性定数を決定した基板の片面に薄膜を成膜した後，再度共鳴周波数の測定を行い，今度は薄膜の弾性定数を未知数として逆計算を行って薄膜の弾性定数を決定します．　薄膜の膜厚はSEMによる断面観察やX線反射率法を用いて決定します．　密度に関しては測定が困難であるため，バルクの値を使用しています．　測定の詳細なフローチャートはFig.3に示します．

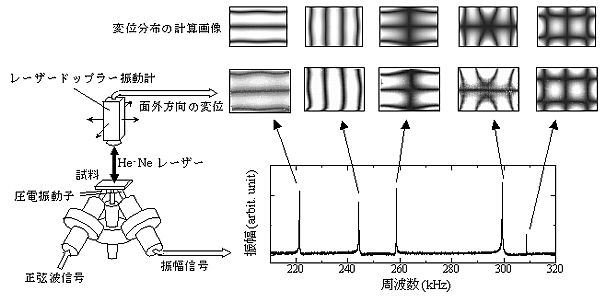
　共鳴周波数の測定には本研究室で考案した3点支持型の圧電センサを使用します（Fig.4）．　このセンサは2本の圧電振動子と1本の熱電対で構成されており，試料を3点の上に置いて測定を行います．　一方の圧電振動子に正弦波信号を入力すると，入力信号と同じ周波数で圧電振動子が振動して試料に振動が励起されます．　試料の振動振幅はもう一方の圧電振動子で電気信号として受信されます．　入力信号の周波数を変えながら振動振幅を測定すると，試料の共鳴数波数と一致する周波数のときに振動振幅が急激に大きくなり（共振状態），スペクトルにピークが現れます．　このピークの位置から共鳴周波数を決定します．　超音波センサではしばしば音響結合材を必要としますが，この3点支持型センサでは音響結合材が必要がなく，試料には自重以外の外力が作用しないためにほぼ完全な自由振動を励起することが可能です．　実際の測定では，振動エネルギーの空気中への漏洩と温度変化による周波数のばらつきを防ぐために真空中かつ一定温度（30℃）の環境下で測定を行います．　このとき，試料を置き直して何度も共鳴周波数を測定をしたときの共鳴周波数のばらつきは　5.0×10-2　以下になります．

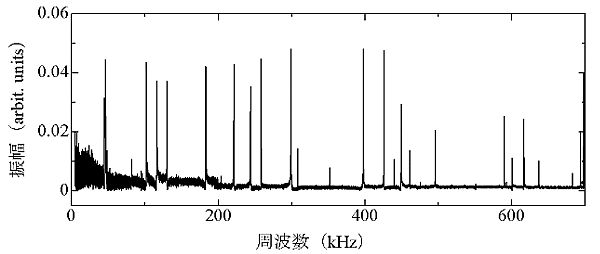
固体の自由振動の共鳴周波数は無数に存在しますが，逆計算によって弾性定数を決定するには同一振動モードの共鳴周波数について計算値と測定値を比較しなければなりません．　振動モードの同定を誤ると真の弾性定数を得ることはできません．　計算においては共鳴周波数と対応する振動モードを同時に知ることができますが，測定では得られた共鳴周波数の振動モードを知る方法はありません．　そこで本研究室では試料表面における面外変位の振動振幅の分布をレーザードップラー振動計を用いて可視化することにより振動モードの同定を実現しました．　Fig.6に測定した試料表面の振動振幅分布画像と，計算で得られた分布画像を示します．　両者は非常に良く一致しており，誤りが起こりえない振動モード同定を裏付けています．　このように，RUS法とレーザードップラー振動計による振動モードの同定を組み合わせた手法がRUS/LDI法です．

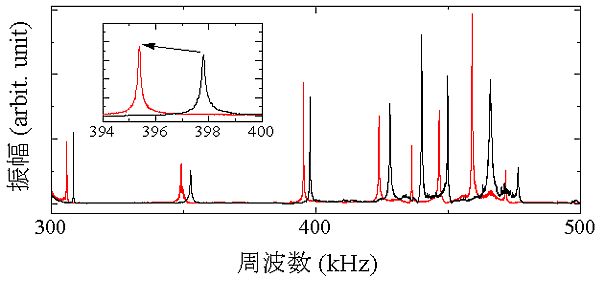
弾性定数の計測においては薄膜の膜厚の測定誤差が最も大きい誤差因子となります．　我々はSEMによる断面観察やX線反射率法を用いて膜厚を決めますが，これらの手法で得られる膜厚には数%程度の誤差が含まれています．　膜厚誤差がもたらす弾性定数の誤差は，弾性定数によって多少異なりますが，およそ5%です．　また，共鳴周波数の測定誤差が測定結果に及ぼす影響は，弾性定数の共鳴周波数に対する寄与率に依存します．　弾性定数の共鳴周波数に対する寄与率は計算によって求めることが可能であり，薄膜の場合は面内方向の引張り応力やせん断応力に関係するC11，C66，C13の寄与が大きく，面外方向の変形に関係するC33とC44の寄与は小さい値となります．　このことから，前者の3つの弾性定数はRUS/LDI法で決定することができます．後者の2つの弾性定数についてはRUS/LDI法で精度良く決定することは容易ではありませんが，C33はピコ秒レーザー超音波を使うことで測定することが可能ですので，C11とC33の関係から薄膜の弾性異方性について議論することができます．

＜参考文献＞

• N. Nakamura, T. Nakashima, S. Oura, H. Ogi, and M. Hirao, Ultrasonics (2009) in press.
• N. Nakamura, H. Ogi, M. Hirao, and T. Ono, Appl. Phys. Lett. 86 (2005) 111918.
• N. Nakamura, H. Ogi, M. Hirao, and T. Ono, J. Appl. Phys. 97 (2005) 013532.
• N. Nakamura, H. Ogi, M. Hirao, and T. Ono, J. Appl. Phys. 97 (2005) 013532
• N. Nakamura, H. Ogi, and M. Hirao, Acta Mater. 52 (2004) 765.
• H. Ogi, G. Shimoike, M. Hirao, K. Takashima, and Y. Higo, J. Appl. Phys. 91 (2002) 4857.
• H. Ogi, K. Sato, T. Asada, and M. Hirao, J. Acoust. Soc. Am. 112 (2002) 2553.

（最終更新日：2009/08/31）