電磁超音波共鳴による

SiCf/Ti複合材の弾性定数と内部摩擦の測定

１．はじめに

複合材料･金属間化合物･セラミックス･生体材料など，今日，新材料の開発がめまぐるしく展開しているなかで，それらの力学的性質の把握は実用上極めて重要です．特に，弾性定数はあらゆる構造物の設計に欠かすことができないため，新材料が開発されるとすぐに必要とされます．また，弾性定数は基本的には原子間ポテンシャルを反映する量であり，金属物性評価にも利用されます．

弾性定数の動的測定法には古くから棒の共振法やパルスエコー法がありますが，固体の結晶対称性が低い場合，これらの測定法では容易に測定が行えません．というのは，例えば，斜方晶系の結晶の場合，独立な弾性定数は９つ存在しますが，これらをすべて決定するためには，棒の共振法で方位の異なる９つの試料が，パルスエコー法では少なくとも４つの試料が必要となるからです．薄膜やワイヤー，薄板，そして小さなサイズしか作れない単結晶などに対しては，方位の異なる試料を切り出すことは難しく，測定できるとしても，特定の弾性定数だけに限られます．一般に，このような形状を持つ材料ほど異方性が強く，独立な弾性定数の数も増します．

この問題を解決すべく考案された手法が，超音波共鳴法（Resonance Ultrasound Spectroscopy：RUS）[1,2]です．直方体，球，円柱など，規則形状を持つ試料を２つの圧電振動子で挟み，一方から連続正弦波を入射し，他方で変位振幅を受信します．送信周波数をスウィープすると，受信振幅は，固体の自由振動の共鳴周波数でピークを示します．共鳴ピークは数多く存在し，個々の共鳴周波数は試料の密度と寸法，弾性定数に依存します．密度と寸法を計測しておき，測定値と最も近い共鳴周波数群を与える弾性定数を逆計算で求め，すべての弾性定数を決定するのです．この手法の利点は，一個の試料に対し一回の実験（周波数スウィープ）によって，すべての独立な弾性定数を決定できることと，1mm 角以下の小さい試料にでも適用できることです．しかし，重大な欠点もあります．それは，測定した共鳴周波数と計算した共鳴周波数のモードの対応の難しさです．例えば直方体の場合，８つの振動グループが存在し[2]，観測される共鳴周波数は，すべてこれらの基本･高次モードです．計算した共鳴周波数のモードは正確に分かっているため，それと同一モードの測定値とを比較しなければならないのですが，通常のRUSでは８つのグループが重畳して観測されるため，その作業は容易ではないのです．特に，高い周波数領域ほど高次モードの数が増加し，共鳴ピークが多数重なり合い，モード特定は困難を極めます．振動モードの対応が正確でなければ，もちろん，逆計算の結果得られた弾性定数は物理的意味を持ちません．

そこで，RUSを大きく発展させた新しい非接触計測法である電磁超音波共鳴（Electromagnetic Acoustic Resonance: EMAR）を考案しました．この手法では，電磁気的作用によって非接触で固体を振動させ，特定の振動グループを選択して共鳴周波数の測定を行うことができます．試料内に直接振動源を生み出すため音響結合剤を必要とせず，高温環境における測定も比較的容易です．また，非接触測定は，接触に関わる振動エネルギの損失を防ぐことができ，内部摩擦の測定には理想的です．本報では，電磁超音波共鳴の原理と，この手法を利用してSiC繊維強化Ti合金複合材料の弾性定数と内部摩擦を室温から1000 Kまで測定した結果について紹介します．

２．材料


測定に用いた複合材は，Ti-6Al-4V多結晶をSCS-6 SiC繊維で強化したものです．高温においても高強度と高靭性を示し，航空宇宙機器の構造用材料として期待されています[3]．図1に示すように，一方向に繊維強化した試料と２つの主軸方向に交互に強化したクロスプライの試料を用いました．それぞれ，Material U とMaterial Xと呼ぶことにします．ともに，SiC繊維薄膜とTi合金薄膜を交互に重ね合わせ（８層），900℃の高温環境下で65 MPaで加圧した後，炉冷して制作したもので，SiC繊維の体積分率はともに0.35です．図１下の写真に示すようにSiC繊維は中心部に炭素心材を含んでいます．試料の製造工程から，Material U は斜方晶，Material Xは正方晶の弾性対称性を持つと考えられ，故に，それぞれ９つと６つの独立な弾性定数を有すると考えられます．試料サイズと密度を表1に示します．

表1 試料寸法と密度

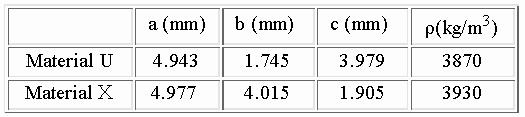
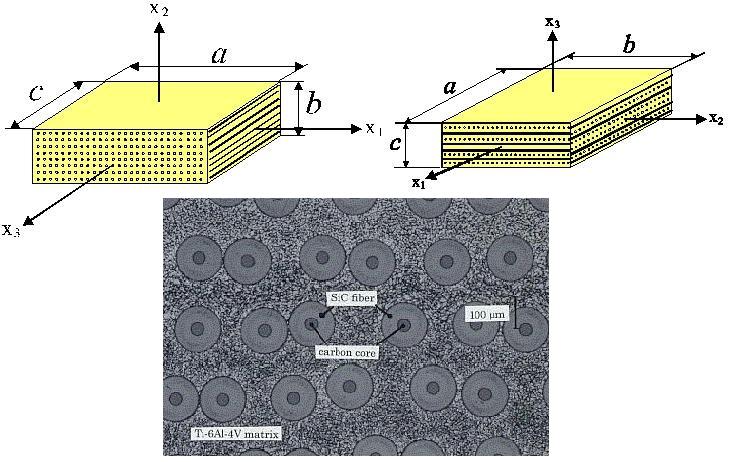
図1 ＳｉＣ繊維強化Ｔｉ合金複合材の層構造と座標系．左：一方向強化試料（Ｍａｔｅｒｉａｌ Ｕ），右：クロスプライ試料（Ｍａｔｅｒｉａｌ Ｘ）

３．測定方法
3.1 電磁超音波共鳴によるモード選択の原理
RUSの欠点を克服するためには，８つのグループの振動を独立に励起･受信することが最も効果的です．そうすることで，モードの重畳を防ぐことができるからです．これは以下に説明する手法によって可能となります．

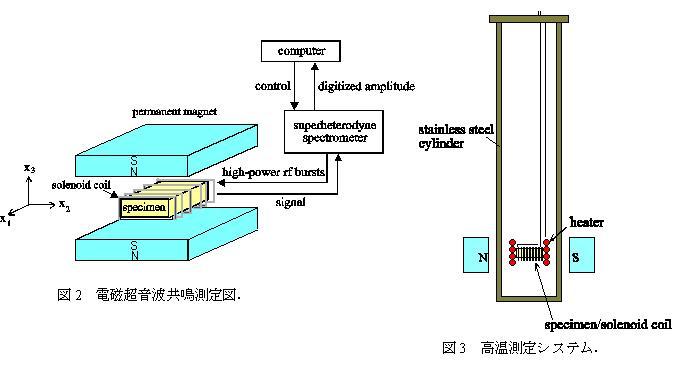
ソレノイドコイル内に試料を挿入し，外部から静磁場を印加する（図2）．コイルに高周波電流を流し，試料表面に渦電流を発生させます． 渦電流と静磁場の相互作用によってローレンツ力が生じ，これを音源として試料を振動させます．受信は送信の逆効果によって同じコイルで行います．ローレンツ力の方向は，静磁場の方向とコイルに流れる電流の方向によって決まるため，これらの幾何学的な関係を操作して試料内の変位の対称性を操り，その結果，発生する振動モードを選択することができます．例えば，図2に示す座標系おいて，渦電流はx1-x2面の試料表面付近をx2方向に流れ，その結果，ローレンツ力はx1-x2面上のx1方向に発生します．ローレンツ力によって，x1方向の変位u1が生じる．u1は上下の試料面で逆方向になるため，同じコイルで変位u1を受信するには，u1は x1とx2に関しては遇関数であり，x3に関しては奇関数でなければなりません．直方体の８つの振動グループのうち，この条件を満足するものはx2軸回りのねじり振動（B2gグループ）だけであり[2]，図2の設定ではこの振動グループに属する振動モードだけを励起することができます．同様に，磁場方向とコイル方向を変えることで，他の振動グループを独立に励起･受信することができます[4, 5]．高温測定では，試料とコイルを円筒形のステンレス容器内に配置し，永久磁石を容器の外側に設置します（図3）．永久磁石を円筒容器の回りに回転させることで磁場方向を変化させ，振動モードを選択することができるのです．

3.2 弾性定数テンソルと内部摩擦テンソルの決定

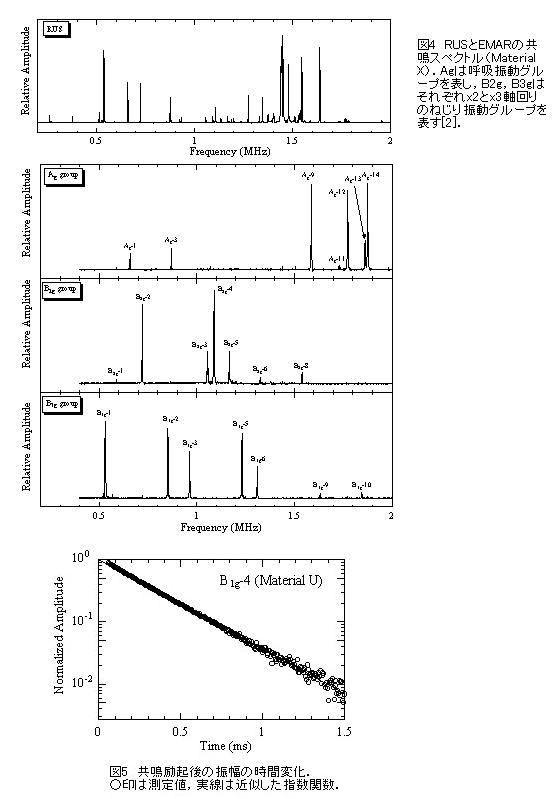
ソレノイドコイルをバースト波信号 (連続正弦波の一部分を取り出した信号) で励起し，ローレンツ力を介して試料を振動させます．励起に続いて，同じコイルが送信の逆過程により，振動変位を受信します．受信信号をスーパーヘテロダイン周波数解析器に送り，駆動周波数と同じ周波数成分の振幅（振幅スペクトル）を抽出します．送信周波数をスウィープし，振幅スペクトルを測定することで，図4に示すような共鳴スペクトルを得ます．共鳴周波数は，スペクトルのピーク近傍のデータにローレンツ関数をフィッティングすることによって得られます．直方体の場合，試料の対称性，密度，寸法，弾性定数が決まれば，自由振動の共鳴周波数を計算できます．逆計算により，測定した共鳴周波数ともっとも近い共鳴周波数を与える弾性定数の組み合わせを決定します [4, 5]．

内部摩擦は自由振動減衰法によって測定します [6] ．コイルに共鳴周波数のバースト波信号を送り，試料内に共鳴状態を作ります．励起を停止し，その後の振動振幅の減少を測定し，指数関数フィッテングにより内部摩擦を決定します．図5に測定例を示します．すべての共鳴モードに対して内部摩擦を測定し，逆計算により個々の弾性定数に対応する内部摩擦テンソルQij-1を決定します [4, 5]．

４．結果と考察

RUSとEMARによって測定した共鳴スペクトルを図4に示します． RUSでは，８つの振動グループが一斉に生じるため，ピークの重畳が特に高周波数側で目立っています．しかし，EMARにおいては，独立に１つの振動グループを励起できるため，ピークは単独に観測され，モードの特定が容易です．EMARとRUSの結果から求めた弾性定数を表2に示します．RUSにおいては，モード特定が困難であったため，逆計算によって決定される弾性定数の値は初期値に大きく左右されました．しかし，EMARで求めた弾性定数の値を初期値として採用することで，良い収束結果を得ました．両者とも，共鳴周波数の測定値と計算値の自乗平均誤差は約0.8%です．比較のため，パルスエコー法によって測定することのできた弾性定数も表2に示します．

EMARとRUSで求めた弾性定数は数%の差で一致しました．Material UのC55に対しては両者の差は大きかったが，この原因は不明である．パルスエコー法の結果も両者と近い値となり，EMARの信頼性を裏付けています．特に，Material Uに関しては繊維の配列からC44>C66 が予測されますが，この傾向はEMARとパルスエコー法の結果には見られますが，RUSの結果は顕著には見られませんでした．

Material Uでは斜方晶系を仮定しましたが，C11～C22, C44～C66, C13～C23であり，ほぼ正方晶系の対称性を持つことがわかります．さらに，C66=(C11-C12)/2の関係が約6%で成り立ち，この誤差範囲で面内等方体（独立な弾性定数は５つ）として扱えます．そこで，Material UとSiC繊維を面内等方体，母材を等方体と仮定し，測定した複合材の弾性定数とTi-6Al-4Vの２つの弾性定数（C11=160.6 GPa，C44=42.0 GPa）[7]から，Mori-Tanakaら[8]の平均場近似の方法を用いてSiC繊維の５つの独立な弾性定数を計算しました．結果を表2に示します． SiC繊維の独立な弾性定数をすべて求めた例は過去にありませんが，長手方向のヤング率は400 GPa～428 GPaと報告されており[9, 10]，本研究で得た値E33=403GPaとよく一致します．

EMARを用いて測定した内部摩擦テンソルを表2に示します．特に注目すべきことは，複合材の層に垂直に伝ぱする弾性波モードに対応するQij-1が他の値を大きく上回っていることです．（例えば，Material Uに対しては，Q22-1>Q11-1,Q33-1，Material XではQ33-1>Q11-1．）これは，複合材の層間の結合が完全ではないことを示唆しています．図6は，Material Xに対して独立な弾性定数を室温から1000 Kの温度域で測定した結果です．温度上昇とともに弾性定数は線形的に減少しますが，約650 Kにおいて変則的な変化を示しました．室温から650 Kの範囲で温度の昇降を行っても，弾性定数は可逆的かつ直線的に変化しましたが，650 Kを超えると，室温まで冷却しても弾性定数は同じ値に戻りませんでした．このことから，650 K付近で内部組織に変化が生じたと考えられる．光学顕微鏡により，1000 Kまで加熱した後の試料を観察した結果，SiC繊維と母材間，さらに，SiC中の炭素心材とSiC間で剥離が見られ，これによって弾性定数が低下したと考えられます．

６．おわりに

本報で紹介した電磁超音波共鳴は異方性の強い微小固体の弾性定数と内部摩擦の測定に有力な手法です．音響結合剤を必要とせず，試料をコイルに挿入するだけで測定を実行できるため，簡便性にも優れています．また，試料の電気伝導性が失われない限り，高温での測定が可能です．非電導体では，表面に導通膜をコーティングすることで同様な測定を行うことができ，本手法の適用は広範囲です．

<<参考文献>>
[1] A. Migliori and J. Sarrao, “Resonant Ultrasound Spectroscopy”, Wiley, New York, 1997.
[2] I. Ohno, J. Phys. Earth 24 (1976), pp. 355-379.
[3] J. Wadsworth and F. H. Froes, JOM 41 (1989), pp. 12-19.
[4] H. Ogi, H. Ledbetter, S. Kim, and M. Hirao, J. Acoust. Soc. Am. 106 (1999), pp. 660-665.
[5] H. Ogi, K. Takashima, H. Ledbetter, M. L. Dunn, G. Shimoike, M. Hirao, and P, Bowen, Acta Mater. 47 (1999), pp. 2787-2796.\\ [6] H. Ogi, M. Hirao, and T. Honda, J. Acoust. Soc. Am. 98 (1995), pp. 2637-2642.\\ [7] E. Naimon, W. Weston, and H. Ledbetter, Cryogenics 14 (1974), pp. 246-249.
[8] T. Mori and K. Tanaka, Acta Metall. 21 (1973), pp. 571-574.
[9] S. K. Mital, C. C. Chamis, and P. K. Gotsis, Comp. Sci. and Tech. 50 (1994), pp. 59-70.
[10] G. T. Ward, D. J. Herrmann, and B. M. Hillberry, J. Comp. Tech. and Res. 17 (1995), pp. 205-211.